Lectura –
Las parábolas matemáticas son útiles en nuestra vida porque nos permiten modelar fenómenos naturales, diseñar estructuras y sistemas eficientes, aplicar principios ópticos, predecir comportamientos económicos y financieros, y desarrollar habilidades cognitivas y matemáticas. Su aplicación abarca una amplia gama de campos y contribuye a nuestra comprensión y mejora del mundo que nos rodea.
Por ejemplo, las parábolas son una herramienta fundamental en la modelización de fenómenos naturales. Muchos procesos en la física, como el movimiento de proyectiles, la trayectoria de objetos en caída libre o la forma de los arcos de agua en una fuente, pueden describirse y predecirse con precisión utilizando ecuaciones y gráficas de parábolas. Las parábolas también se utilizan en la óptica y la tecnología. En la fabricación de espejos parabólicos, por ejemplo, se logra reflejar la luz incidente desde múltiples direcciones hacia un solo punto focal, lo que es esencial en telescopios, reflectores de automóviles y sistemas de energía solar concentrada.
¿Por qué se utilizan parábolas para diseñar antenas?
Las antenas parabólicas son ampliamente utilizadas en la transmisión y recepción de señales de radio, televisión, comunicaciones por satélite y muchas otras aplicaciones. Estas antenas se basan en el principio óptico de las parábolas, que permite la concentración de la energía electromagnética en un punto focal.
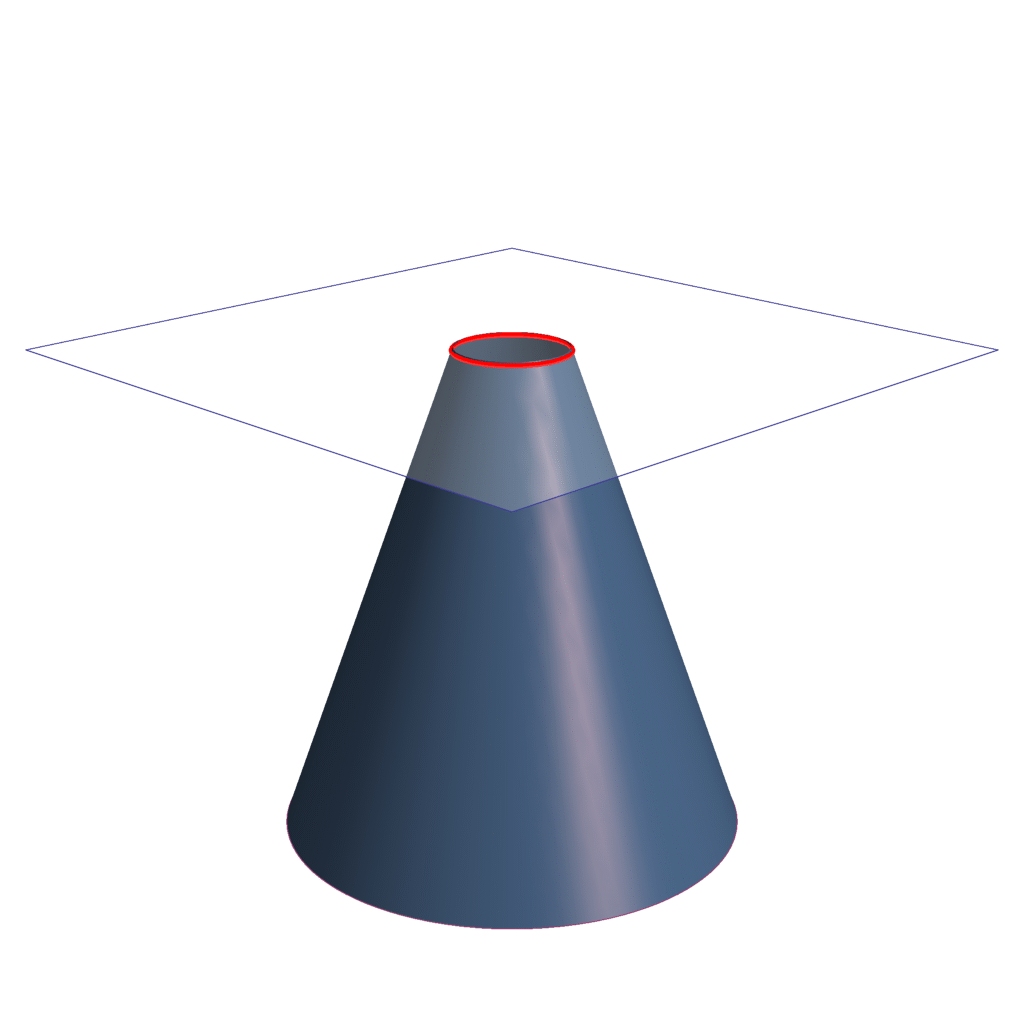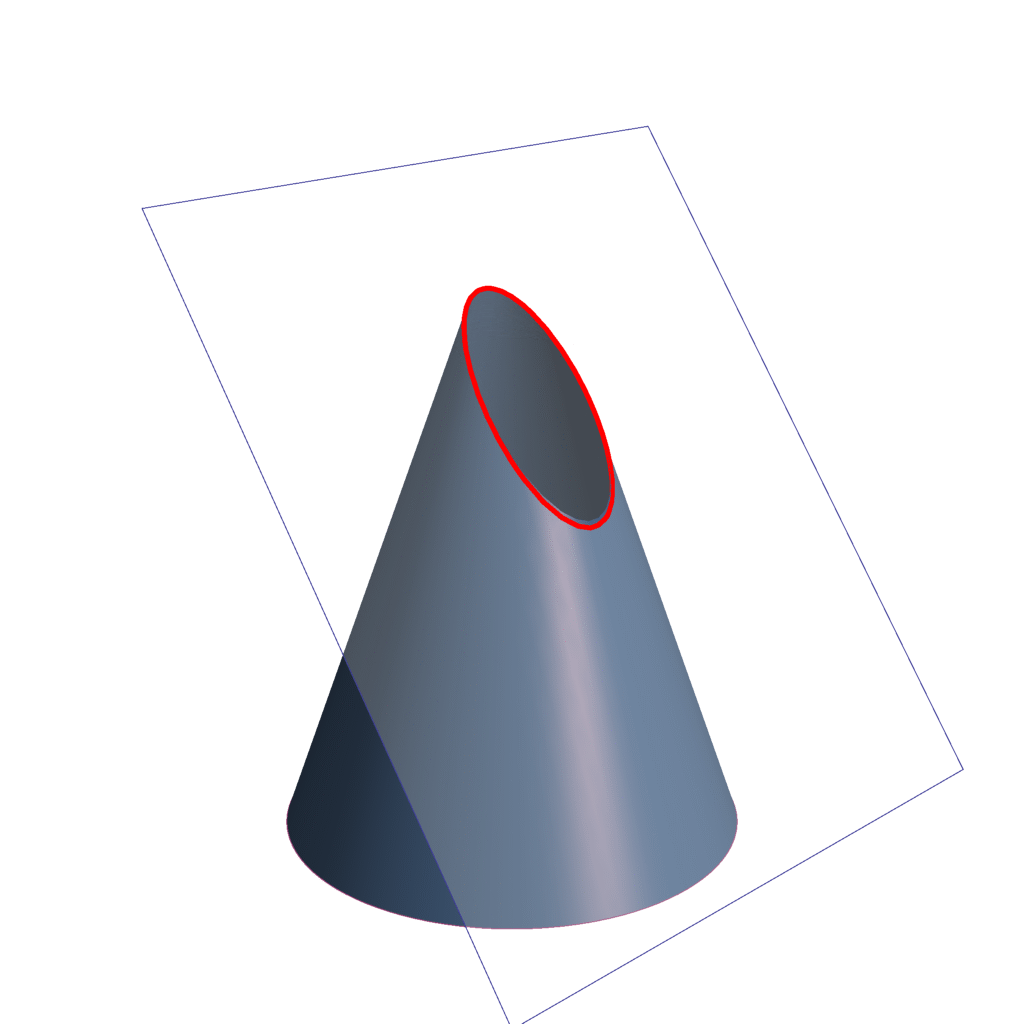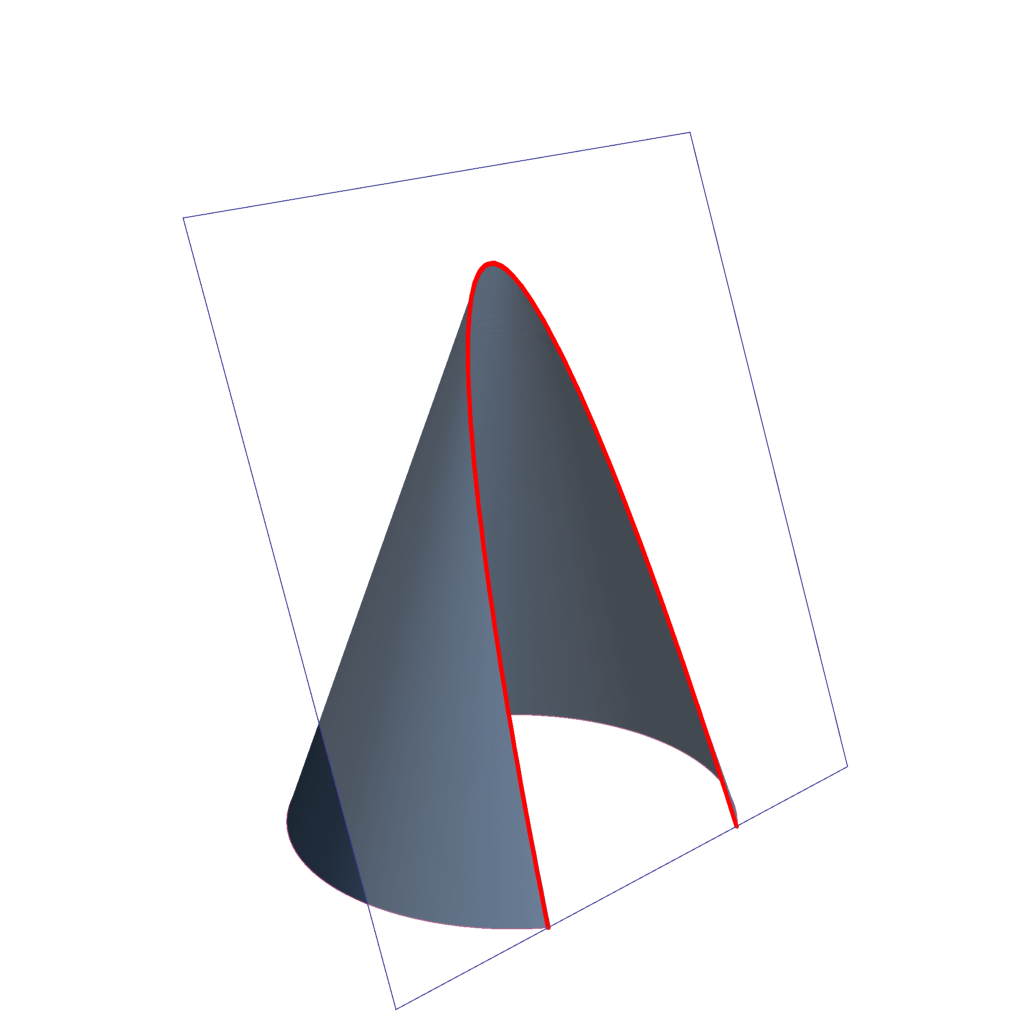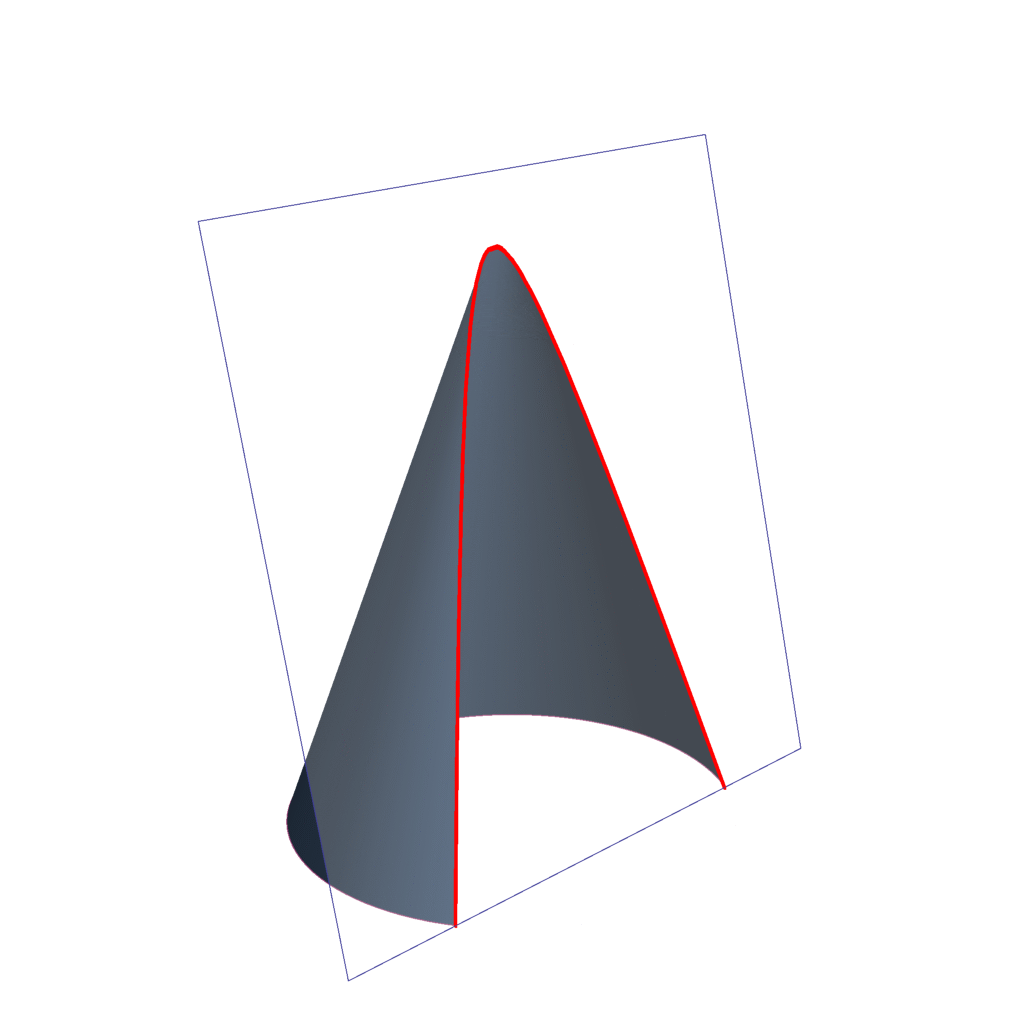
La forma de una parábola es determinada por una curva en la que todos los puntos están equidistantes de una línea llamada directriz y de un punto denominado foco. En el diseño de antenas, la parábola se utiliza para dirigir y enfocar las ondas electromagnéticas hacia el foco, donde se encuentra el receptor o transmisor.
Existen varias razones por las cuales la parábola es la sección cónica preferida en el diseño de antenas:
Propiedades de enfoque: La forma de la parábola permite que las ondas electromagnéticas incidentes se reflejen hacia el foco, lo que resulta en una mayor concentración de energía en comparación con otras secciones cónicas. Esto es esencial para transmitir o recibir señales a largas distancias con alta eficiencia.
Simetría: La parábola tiene una simetría inherente que facilita la construcción de antenas con propiedades de haz simétricas. Esto es especialmente útil en aplicaciones de comunicaciones donde se busca una propagación uniforme de la señal.

Reducción de aberraciones: La parábola es capaz de minimizar las aberraciones, lo que significa que los rayos electromagnéticos que inciden en diferentes puntos de la antena convergen de manera más precisa en el foco. Esto mejora la calidad de la señal y reduce la distorsión.
Apertura efectiva: La forma parabólica permite una mayor apertura efectiva de la antena en comparación con otras geometrías. La apertura efectiva es una medida de la capacidad de la antena para capturar señales entrantes, y una mayor apertura efectiva resulta en una mayor sensibilidad y ganancia.
Diseño mecánico: La forma de la parábola es relativamente fácil de fabricar y construir, lo que la convierte en una opción práctica en términos de diseño y fabricación de antenas. Además, su forma simple facilita el cálculo y ajuste de los parámetros necesarios para el rendimiento óptimo de la antena.
La forma parabólica ofrece ventajas significativas en términos de enfoque, simetría, reducción de aberraciones, apertura efectiva y facilidad de diseño. Estas características hacen de la parábola la mejor sección cónica para el diseño de antenas en una amplia gama de aplicaciones de comunicaciones.
¿Qué otras aplicaciones tiene la parábola?
Las parábolas se utilizan en el diseño de puentes colgantes debido a las propiedades estructurales y de distribución de cargas que ofrecen. Aunque no todos los puentes colgantes tienen una forma de parábola perfecta, se basan en los principios geométricos y estructurales de esta curva.
Las parábolas tienen la propiedad de que cualquier carga aplicada en su superficie se distribuye uniformemente a lo largo de la curva. Esto es beneficioso en un puente colgante, ya que las cargas, como el peso de la estructura, el tráfico y las fuerzas del viento, se distribuyen de manera más uniforme a lo largo de los cables de suspensión.
Otro aspecto para considerar es la forma de la parábola permite que los cables principales del puente colgante se mantengan en tensión constante. La carga aplicada en los extremos del puente se transmite a lo largo de los cables de suspensión y se distribuye a lo largo de la curva de manera uniforme. Esto ayuda a minimizar la aparición de momentos de flexión y proporciona una mayor estabilidad y resistencia a la estructura del puente.
Además de las consideraciones estructurales y funcionales, las parábolas también se eligen en el diseño de puentes colgantes por razones estéticas. La forma curva y elegante de una parábola crea un aspecto visualmente atractivo y armonioso, lo que contribuye a la apreciación estética de la estructura del puente.
