Lectura – Funciones de varias variables y su poder descriptivo
¿Qué son las funciones de varias variables?
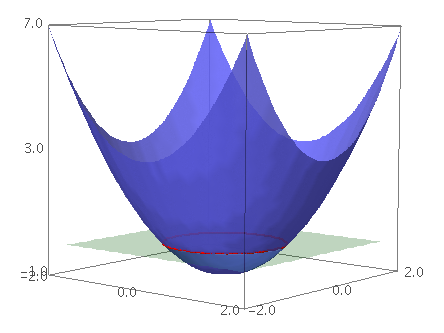
Las funciones de varias variables son funciones matemáticas que toman más de una variable como entrada y devuelven un valor como salida. Estas funciones son una extensión de las funciones de una sola variable, donde solo hay una variable independiente. En el caso de las funciones de varias variables, hay dos o más variables independientes.
Una función de dos variables, por ejemplo, se denota comúnmente como f(x, y), donde x e y son las variables independientes. La función asigna a cada par ordenado de valores (x, y) un único valor z, que es la variable dependiente. El gráfico de una función de dos variables generalmente se representa en un espacio tridimensional, donde los ejes x, y, y z representan las tres dimensiones.
¿Cuáles son las aplicaciones de las funciones de varias variables?
Las funciones de varias variables se utilizan en diversas disciplinas, como matemáticas, física, economía, ingeniería y muchas otras, para modelar fenómenos del mundo real que dependen de más de una variable. Los conceptos asociados con las funciones de varias variables incluyen tasas de cambio parciales, derivadas parciales, puntos críticos, máximos y mínimos, entre otros.
Por ejemplo, la función de varias variables f(x, y) = x^2 + y^2 representa una superficie parabólica en tres dimensiones. Cada punto (x, y) en el plano xy se mapea a un valor z de acuerdo con la fórmula de la función. Explorar y entender estas funciones es fundamental para el análisis matemático y la modelización de fenómenos del mundo real.
¿Cómo se llegó al desarrollo de funciones en varias variables?
El desarrollo de las funciones de varias variables está vinculado a la evolución del cálculo y el análisis matemático a lo largo de la historia.

En el siglo XVII, los matemáticos como Isaac Newton y Gottfried Wilhelm Leibniz desarrollaron el cálculo diferencial, que se centraba inicialmente en funciones de una sola variable. Este fue un paso crucial en el desarrollo de herramientas matemáticas para comprender las tasas de cambio y las derivadas.
A medida que avanzaba el cálculo, los matemáticos empezaron a explorar funciones de más de una variable. El matemático francés Augustin-Louis Cauchy, a principios del siglo XIX, contribuyó al desarrollo de las derivadas parciales y definió conceptos como la continuidad y la diferenciabilidad para funciones de varias variables.
El matemático alemán Carl Gustav Jacob Jacobi y otros contribuyeron al teorema de las funciones implícitas, que proporciona condiciones bajo las cuales una ecuación puede ser implícitamente definida por una función. Este teorema fue crucial para el estudio de ecuaciones que relacionan múltiples variables.
En el siglo XIX, el cálculo vectorial también se integró en el estudio de funciones de varias variables. Matemáticos como Hermann Grassmann y Josiah Willard Gibbs desarrollaron conceptos como el gradiente, la divergencia y el rotacional, que son fundamentales en el análisis de funciones de varias variables.
Durante el siglo XIX, matemáticos como Augustin-Louis Cauchy, Bernhard Riemann y Karl Weierstrass trabajaron en teoremas que extendían el análisis de funciones a varias variables. Estos incluyen el Teorema de la Función Inversa y el Teorema de la Función Implícita, que proporcionan condiciones bajo las cuales se pueden encontrar funciones inversas y expresar ciertas ecuaciones de manera implícita, respectivamente.
¿Cómo se aplican las funciones de varias variables en la física?
En la física, se utilizan diversas funciones de varias variables para modelar y describir fenómenos naturales. Estas funciones son esenciales para entender y predecir el comportamiento de sistemas físicos complejos. Aquí hay algunas funciones importantes de varias variables en física:
Función de Onda en Mecánica Cuántica:
En la mecánica cuántica, la función de onda es fundamental. Es una función de varias variables que describe el estado cuántico de un sistema. La magnitud al cuadrado de la función de onda proporciona la probabilidad de encontrar una partícula en una posición y momento dados.

Campo Escalar y Vectorial:
En muchas teorías físicas, como la electrostática y la magnetostática, se utilizan campos escalares y vectoriales. Estos campos son funciones de varias variables que asignan un valor escalar o vector a cada punto en el espacio, representando la distribución de carga eléctrica, densidad de masa, etc.
Ecuaciones de Maxwell:
Las ecuaciones de Maxwell describen el comportamiento del campo electromagnético. Son un conjunto de ecuaciones diferenciales parciales que involucran funciones de varias variables, como el campo eléctrico y el campo magnético, en función del espacio y el tiempo.
Tensor de Energía-Momento:
En la relatividad general, el tensor de energía-momento es una función de varias variables que describe la distribución de energía y momento en el espacio-tiempo. Es crucial para entender la curvatura del espacio-tiempo y la dinámica de los campos gravitatorios.
Funciones de Legendre:
Las funciones de Legendre son soluciones de la ecuación diferencial asociada con los polinomios de Legendre. Estas funciones son importantes en el contexto de problemas de simetría esférica. Se utilizan en física para describir fenómenos que exhiben simetría esférica, como el estudio del potencial electrostático y el campo gravitatorio en esferas.
Funciones de Hermite:
Las funciones de Hermite son soluciones de la ecuación diferencial asociada con los polinomios de Hermite. Estas funciones son fundamentales en la descripción de sistemas cuánticos y en el análisis de procesos estocásticos. Se utilizan en la cuantización de osciladores armónicos, describen estados cuánticos de partículas en un potencial cuadrático, y también son relevantes en la teoría de probabilidad.
Armónicos Esféricos:
Los armónicos esféricos son funciones que surgen al expandir funciones escalares en coordenadas esféricas. Representan las simetrías rotacionales de un sistema. Son esenciales en problemas con simetría esférica, como la expansión de funciones en campos gravitatorios y electrostáticos. También se utilizan en la descripción de campos electromagnéticos y en problemas relacionados con la mecánica cuántica.
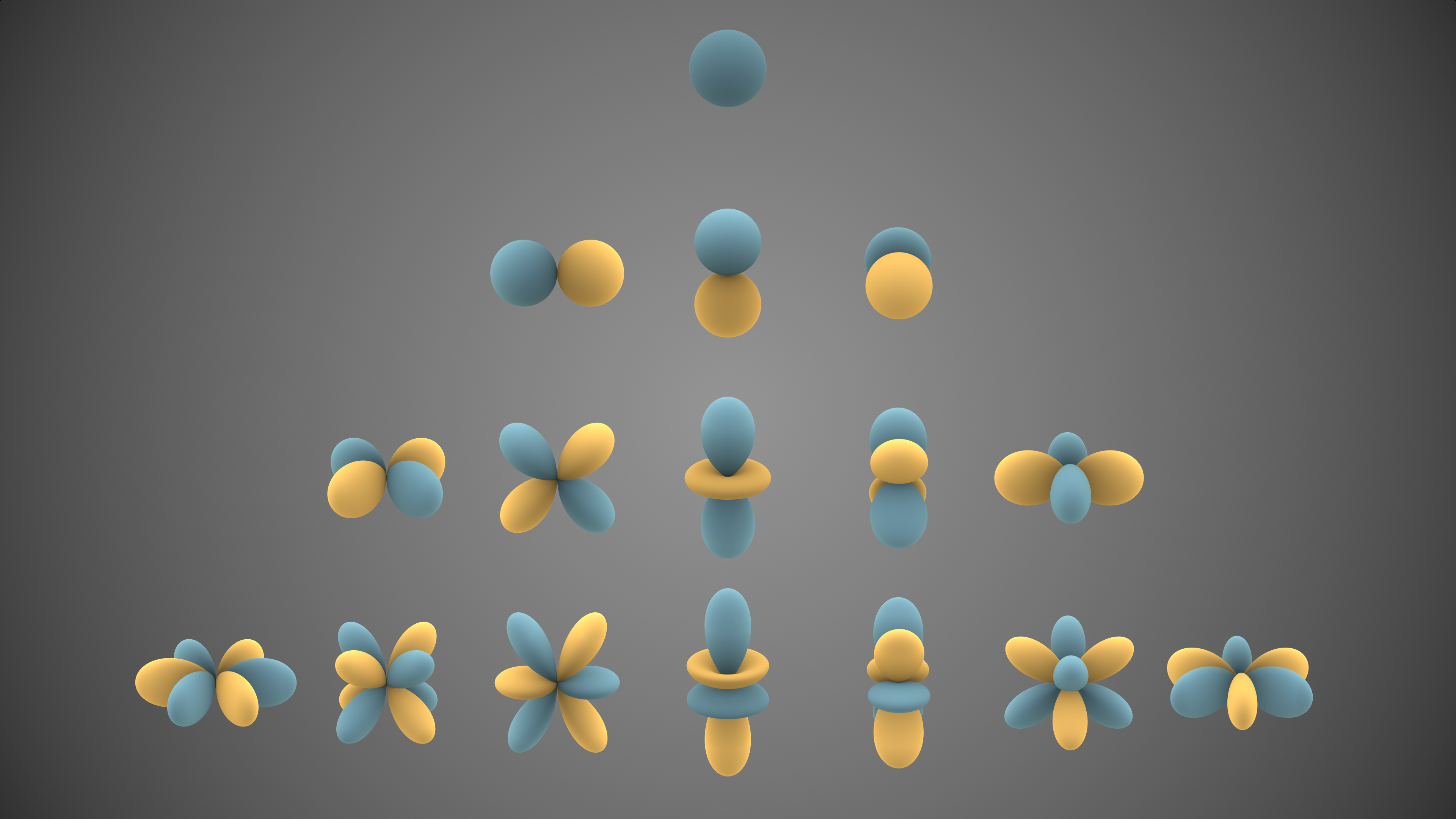
En resumen, estas funciones especiales son herramientas matemáticas poderosas que surgen en la resolución de ecuaciones diferenciales en física y matemáticas aplicadas. Su utilidad radica en su capacidad para describir y modelar fenómenos que exhiben ciertas simetrías y patrones. Desde sistemas cuánticos hasta problemas de campos físicos, estas funciones desempeñan un papel clave en la comprensión y la resolución de una variedad de problemas en la física y disciplinas relacionadas.
