Lectura – 2da ley de Newton: una ecuación con derivadas
¿Cómo ayudan las derivadas a la física?
Las derivadas nos proporcionan una herramienta matemática poderosa para analizar cómo cambian las cantidades físicas en función del tiempo. La relación entre la fuerza, la masa, la aceleración y la velocidad de un objeto en movimiento se puede expresar y entender mejor mediante derivadas.
Las derivadas nos permiten abordar situaciones físicas más complicadas, como sistemas de partículas en movimiento, fuerzas variables con el tiempo o trayectorias curvas. Al utilizar conceptos avanzados de cálculo, como derivadas parciales y ecuaciones diferenciales de segundo orden, podemos resolver problemas complejos de dinámica y cinemática en la física.
Gracias a las derivadas, podemos cuantificar y predecir el comportamiento de los objetos bajo la influencia de fuerzas y resolver una amplia gama de problemas en la física clásica.
¿Cómo se aplican a la segunda Ley de Newton?
La Segunda Ley de Newton es una de las leyes fundamentales de la física clásica que describe cómo un objeto se mueve cuando se aplica una fuerza sobre él. Esta ley se puede expresar matemáticamente utilizando derivadas, lo que nos permite entender cómo la velocidad y la aceleración de un objeto cambian en respuesta a la fuerza aplicada.
La formulación matemática de la Segunda Ley de Newton con derivadas es la siguiente:
F = m \cdot \frac{d^2x}{dt^2} Donde:
- F es la fuerza neta aplicada sobre el objeto
- m es la masa del objeto
- \displaystyle\frac{d^2x}{dt^2} representa la segunda derivada de la posición x respecto al tiempo t . Esto corresponde a la aceleración del objeto
Para comprender mejor esta ecuación, desglosemos su significado:
- La fuerza F se define como el producto de la masa del objeto y su aceleración
- La aceleración \frac{d^2x}{dt^2} representa cómo cambia la velocidad del objeto con respecto al tiempo. Si la aceleración es positiva, el objeto aumentará su velocidad en la dirección de la fuerza aplicada. Si la aceleración es negativa, el objeto disminuirá su velocidad en dirección opuesta a la fuerza. Si la aceleración es cero, el objeto mantendrá su velocidad constante.
- La masa m del objeto es una propiedad intrínseca del mismo y determina su inercia, es decir, la resistencia que opone al cambio de movimiento cuando se le aplica una fuerza. Cuanta mayor sea la masa, más difícil será cambiar su velocidad, y viceversa.
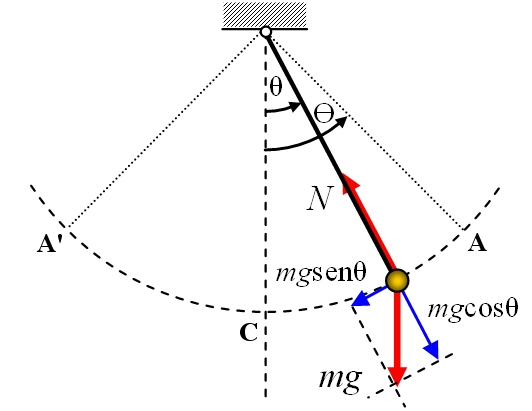
Es importante mencionar que la Segunda Ley de Newton es válida para sistemas donde las velocidades son mucho menores que la velocidad de la luz y las masas son macroscópicas. Para situaciones en las que las velocidades son comparables a la velocidad de la luz o las masas son extremadamente grandes (como en el ámbito de la física relativista o la cosmología), se requieren formulaciones más avanzadas de la dinámica.
