Lectura – Principio de Fermat, geodésica y braquistócrona: mínimos en la naturaleza
¿Qué es el principio de Fermat?

El Principio de Fermat, en honor a Pierre de Fermat, es un principio fundamental en óptica que establece que la luz sigue el camino óptico más rápido entre dos puntos en un medio con una velocidad de propagación constante. El principio fue formulado por Pierre de Fermat en el siglo XVII y es uno de los principios básicos que rigen el comportamiento de la luz en la teoría de la reflexión y refracción.
En términos más simples, el Principio de Fermat establece que cuando la luz viaja de un punto a otro en un medio con una velocidad constante (como el aire o el vidrio), seguirá la trayectoria que minimiza el tiempo de viaje entre esos dos puntos. En otras palabras, la luz elige el camino más rápido para llegar de un punto a otro.
Este principio es una consecuencia directa del principio de mínima acción en física. La luz, como todas las partículas y ondas, busca seguir una trayectoria que minimice la acción (que en el caso de la luz está relacionada con el tiempo) entre dos puntos.
Es importante tener en cuenta que el Principio de Fermat es válido para medios homogéneos y no se aplica a medios con variaciones significativas en su índice de refracción. Para tales medios, se requiere una formulación más general del principio, conocida como el Principio de Fermat generalizado o el Principio de Fermat-Huygens.
¿Qué es una geodésica?
Una geodésica es una curva o trayectoria que representa la distancia más corta o el camino de menor longitud entre dos puntos en una superficie o en un espacio curvo. En otras palabras, es el equivalente geométrico del concepto de línea recta en espacios planos o euclidianos.
En el contexto de geometría diferencial y teoría de la relatividad, las geodésicas son líneas que siguen la curvatura del espacio-tiempo y representan las trayectorias naturales que los objetos en movimiento libre seguirían sin estar sujetos a fuerzas externas.
Hay tres tipos principales de geodésicas, dependiendo del tipo de superficie o espacio en el que se encuentren:
- Geodésicas en un plano: En un espacio plano o euclidiano, las geodésicas son simplemente líneas rectas que conectan dos puntos. En este caso, la distancia más corta entre dos puntos es una línea recta.
- Geodésicas en una superficie curva: En una superficie curva, como la superficie de una esfera o un cilindro, las geodésicas pueden ser líneas curvas que conectan dos puntos y siguen la curvatura de la superficie. Un ejemplo clásico es la circunferencia más corta que conecta dos puntos en una esfera, conocida como un “círculo máximo”.
- Geodésicas en espacios curvos o relativistas: En la teoría de la relatividad general de Einstein, el espacio-tiempo se curva debido a la presencia de masa y energía. Las geodésicas en este contexto representan las trayectorias seguidas por partículas o fotones en movimiento libre, y se curvan debido a la influencia gravitacional. Los objetos en movimiento siguen estas geodésicas sin necesidad de fuerzas externas.
¿Qué es una braquistócrona?
La braquistócrona es una curva matemática que representa el camino más rápido entre dos puntos en un plano vertical bajo la influencia exclusiva de la gravedad. El problema de la braquistócrona fue propuesto y resuelto por el matemático suizo Johann Bernoulli en 1696.
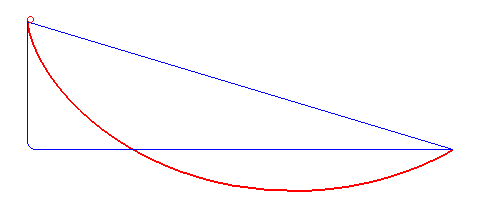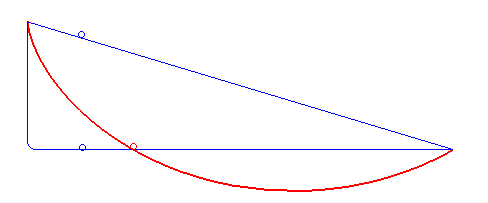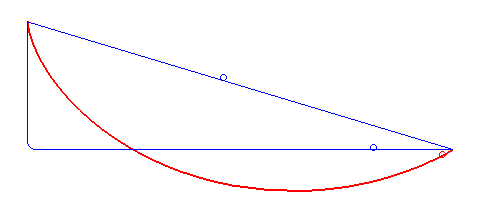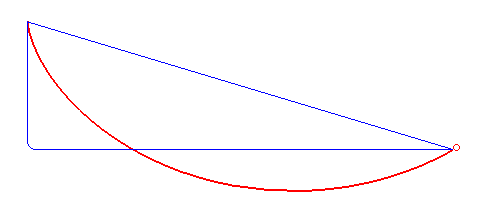
El término “braquistócrona” proviene del griego “brachys” (que significa “más corto”) y “chronos” (que significa “tiempo”), lo que indica la naturaleza del problema: encontrar la curva más corta o rápida entre dos puntos en un plano vertical, considerando únicamente la fuerza gravitacional.
La solución a la braquistócrona es una curva específica llamada “cicloide”. La cicloide es la trayectoria que describe un punto en la circunferencia de una rueda que rueda sin deslizar sobre una superficie mientras recorre un camino determinado. La característica interesante de la cicloide es que cualquier punto en ella alcanza el punto más bajo en el mismo tiempo, independientemente de dónde haya comenzado en la curva.
Esta propiedad especial de la cicloide garantiza que cualquier objeto que se mueva a lo largo de la braquistócrona llegará del punto de partida al punto de llegada en el menor tiempo posible bajo la acción exclusiva de la gravedad. Es decir, la cicloide representa la trayectoria óptima que minimiza el tiempo de llegada.
Estos principios y conceptos son fundamentales en la física y las matemáticas, y juegan un papel importante en la comprensión de los fenómenos naturales y la optimización de sistemas en la naturaleza. Desde la propagación de la luz hasta la trayectoria de los objetos bajo la gravedad, estos principios nos ayudan a entender cómo la naturaleza busca eficiencia y economía en sus procesos.
