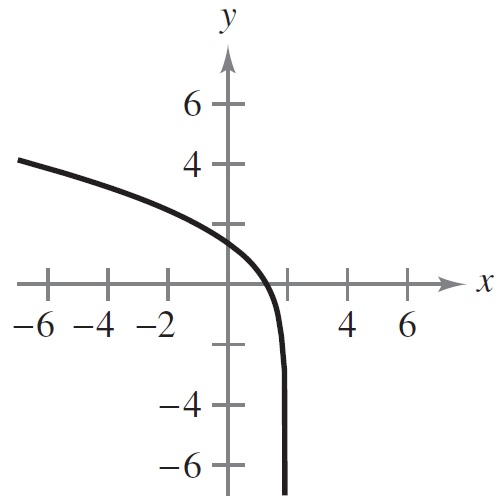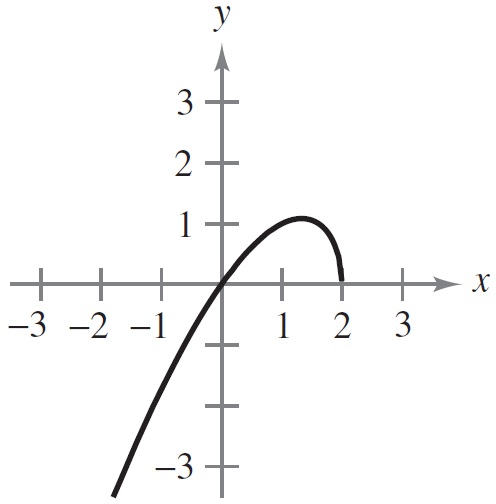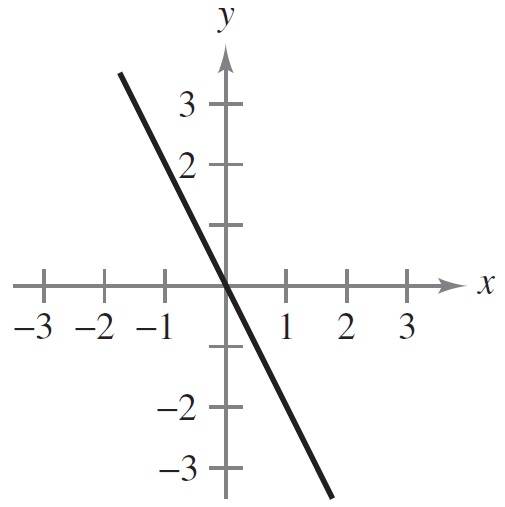Actividad – Análisis gráfico de una función
¡Pon a prueba tus conocimientos!
La siguiente prueba no cuenta con un límite de tiempo, podrás practicar las veces que lo necesites, al finalizar esta actividad podrás conocer los resultados obtenidos. Para que esta prueba se marque como completa deberás de obtener como mínimo un 70% de calificación. Haz clic en “Empezar Cuestionario” para comenzar.
¡Éxito!
Resumen del Cuestionario
0 of 5 Preguntas completed
Preguntas:
Información
Ya has completado el cuestionario anteriormente. Por lo tanto no puedes iniciarlo de nuevo.
Cargando Cuestionario…
Debes iniciar sesión o registrarte para empezar el cuestionario.
En primer lugar debes completar esto:
Resultados
Resultados
0 de 5 Preguntas respondidas correctamente
Tu tiempo:
El tiempo ha pasado
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
| Puntuación media |
|
| Tu puntuación |
|
Categorías
- Sin categorizar 0%
-
¡No te rindas! Afortunadamente puedes seguir intentándolo cuantas veces lo necesites, sigue practicando y muy pronto verás muchas mejoras.
-
¡Casi lo logras! Sigue practicando y muy pronto dominarás el tema.
-
¡Muy bien! Has aprobado esta lección, te recomendamos seguir repasando los temas para que sigas mejorando, recuerda que puedes hacer tantos intentos como quieras.
-
¡Excelente! Tienes un muy buen dominio del tema, estás a nada de obtener un 100%, repasa una vez más el tema y alcanzarás la perfección.
-
¡Muchas felicidades! Has obtenido un 100%, estamos seguros que dominas este tema, pero aun así no dejes de practicar, recuerda que cada cierto tiempo puedes encontrar nuevas preguntas para esta misma actividad.
- 1
- 2
- 3
- 4
- 5
- Actual
- Revisar
- Respondido/a
- Correcto
- Incorrecto
-
Pregunta 1 de 5
1. Pregunta
1 punto(s)Analiza la siguiente función para hacer un bosquejo de su gráfica, y con la información recopilada escribe las respuestas correctas: f(x)=x^4-12x^3+48x^2-64x
*Nota: Todos los puntos escríbelos en orden, comenzando con los que tengan abscisa menor hasta la mayor. Utiliza “-I” para -\infty y “+I” para +\infty
-
Primer cero: x= , y=
Segundo cero: x= , y=
Intersección con eje y : x= , y=
Coordenadas del mínimo o máximo relativo: x= , y=
Primer punto de inflexión: x= , y=
Segundo punto de inflexión: x= , y=
Intervalos de crecimiento: ( , )
Intervalos de decrecimiento: ( , )
Intervalos de concavidad positiva: ( , ) y ( , )
Intervalos de concavidad negativa: ( , )
CorrectoIncorrecto -
-
Pregunta 2 de 5
2. Pregunta
1 punto(s)La figura siguiente muestra la gráfica de una función cuyas primera y segunda derivada existen y están definidas. Determina para cada punto si y' y y'' son positivas, negativas o nulas, escribiendo “+”, “-” o “0” respectivamente.
-
Punto P: y' = , y'' =
Punto Q: y' = , y'' =
Punto R: y' = , y'' =
Punto S: y' = , y'' =
Punto T: y' = , y'' =
CorrectoIncorrecto -
-
Pregunta 3 de 5
3. Pregunta
1 punto(s)A partir de la gráfica mostrada en la siguiente figura, relaciona cada abscisa con el punto crítico correspondiente:
Ordenar elementos
- Mínimo local – Punto estacionario
- Máximo local – Punto estacionario
- Mínimo absoluto – Punto singular
- Máximo absoluto – Punto singular
-
x=a
-
x=b
-
x=c
-
x=d
CorrectoIncorrecto -
Pregunta 4 de 5
4. Pregunta
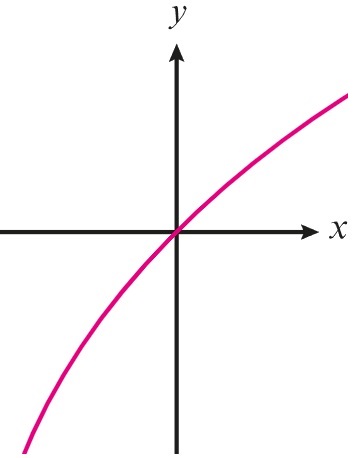
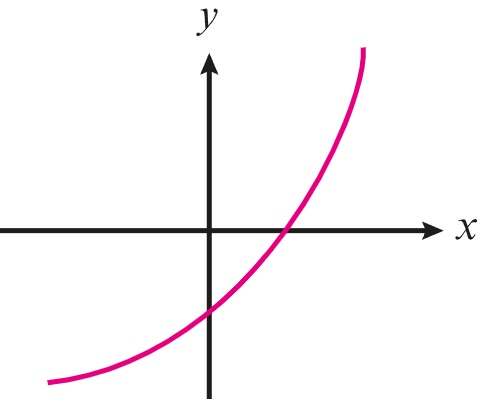
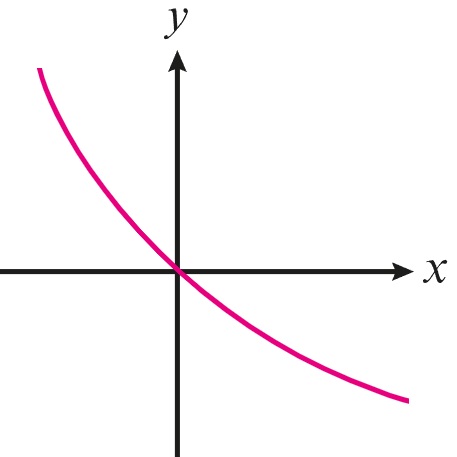
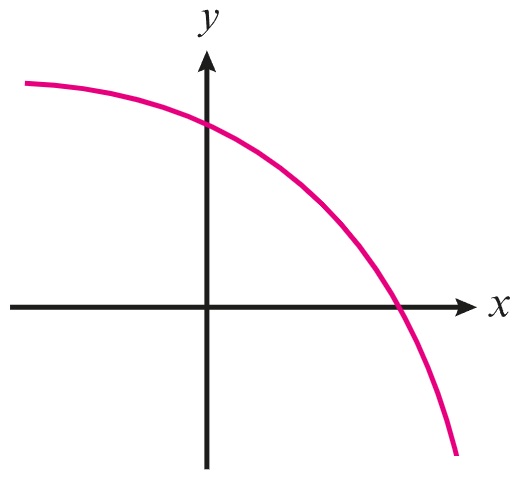
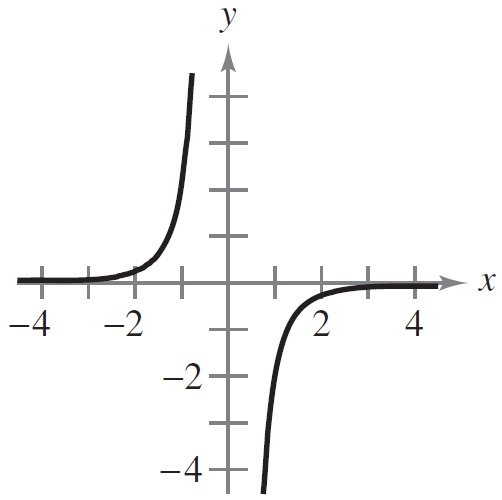
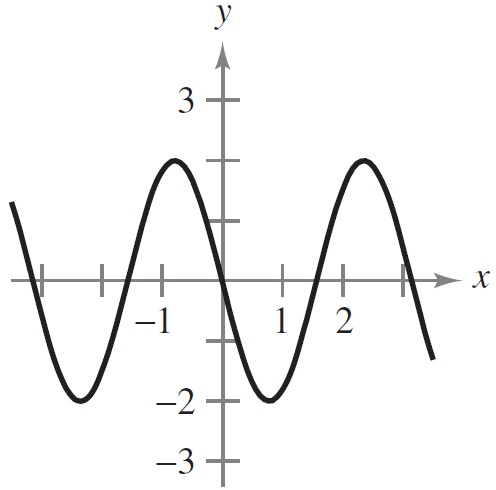
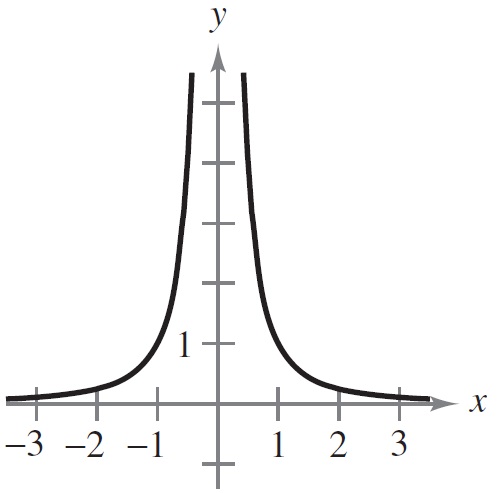
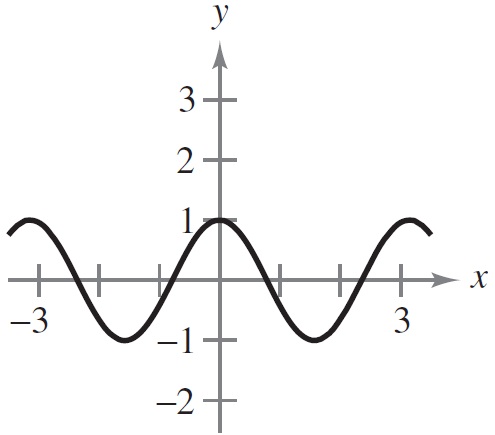
1 punto(s)Relaciona cada gráfica con el enunciado correspondiente.
Ordenar elementos
- La gráfica es creciente y cóncava hacia abajo
- La gráfica es creciente y cóncava hacia arriba
- La gráfica es decreciente y cóncava hacia arriba
- La gráfica es decreciente y cóncava hacia abajo
CorrectoIncorrecto -
Pregunta 5 de 5
5. Pregunta
1 punto(s)A continuación se muestran las gráficas de una función. Selecciona las gráficas de las derivadas y relaciona cada inciso con su respuesta correspondiente.
Ordenar elementos
CorrectoIncorrecto -
